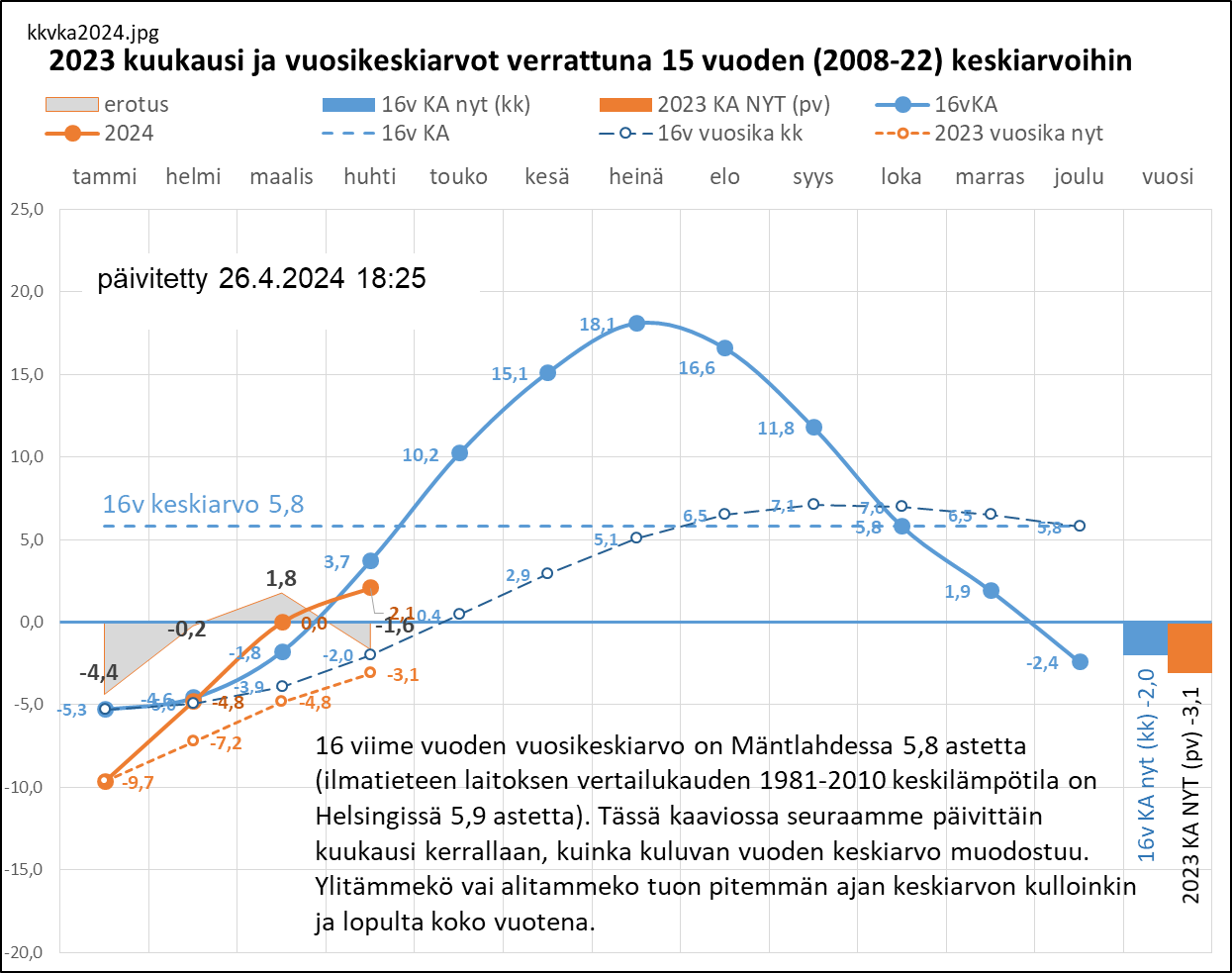
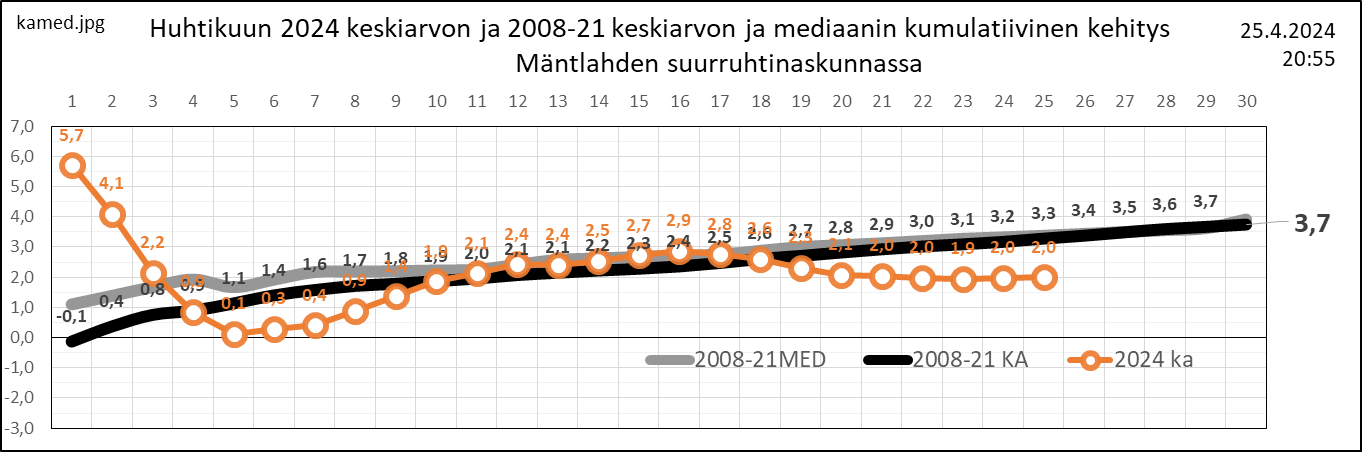
Aritmeettinen keskiarvo
Säätiedotuksissa kuulemme enemmän kuin usein kerrottavan lämpötilojen olevan joko “tavanomaista lämpimämpiä” tai “tavanomaista kylmempiä” ajankohtaan nähden. Tämä tavanomainen lämpötila johdetaan standardiksi sovitusta 30-vuotisesta vertailukaudesta vuosilta 1981-2010, sen aritmeettisesta keskiarvosta. Tarkastelemme tässä kuukausilämpötiloja esimerkkinä Ilmatieteen laitoksen Anjalan sääaseman tilastot. Tammikuu on havainnollinen kuukausi sikäli, että siinä lämpötilavaihtelut ovat suuria. Päivämeteorologiassa käytetään usein lyhyempiä jaksoja, viikon tai jopa yksittäisen päivän 30 vuotista keskiarvoa, mutta periaate on sama ja vaihtelu on päivä- ja viikkoarvoissa vielä suurempaa.
Kuvakaappaus keinulaudasta Aki Taanilan artikkelista (https://analysointi.wordpress.com/keskiarvo/).
Keskiarvoon vertaaminen on aina ongelmallista, sillä keskiarvo ei välttämättä kerro “tavanomaisista”, yleisimmistä lämpötiloista yhtään mitään. Keinulauta vertaus havainnollistaa hyvin (kuva oikealla). Esimerkiksi usein pitkän ajan keskiarvo talvikuukaudesta painottuu muutaman kylmän vuoden vuoksi paljon alemmas kuin yleisin lämpötila on. Jos keskiarvo määrittää tavanomaisen lämpötilan, ei tavanomaista lämpötilaa ilmene kuin poikkeustapauksissa. Oikealla kuvakaappaus keinulaudasta Aki Taanilan artikkelista (https://analysointi.wordpress.com/keskiarvo/).
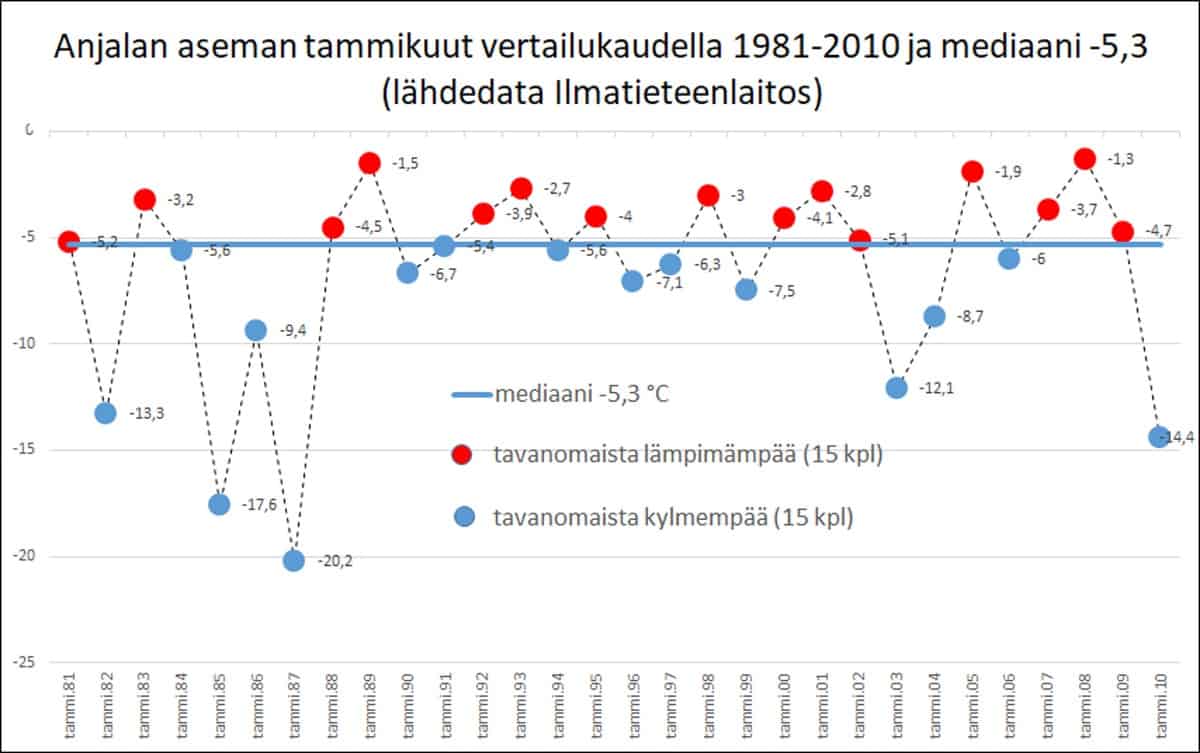
No niin, meillä on siis 30 vuoden ajalta jokaisen tammikuun yhteenlaskettu keskiarvo (-6,6 °C) ja vertaamme sitä nykyisiin lämpötiloihin, mutta katsokaamme millainen kuukausittainen vaihtelu itse tuon vertailukautemme sisällä on.
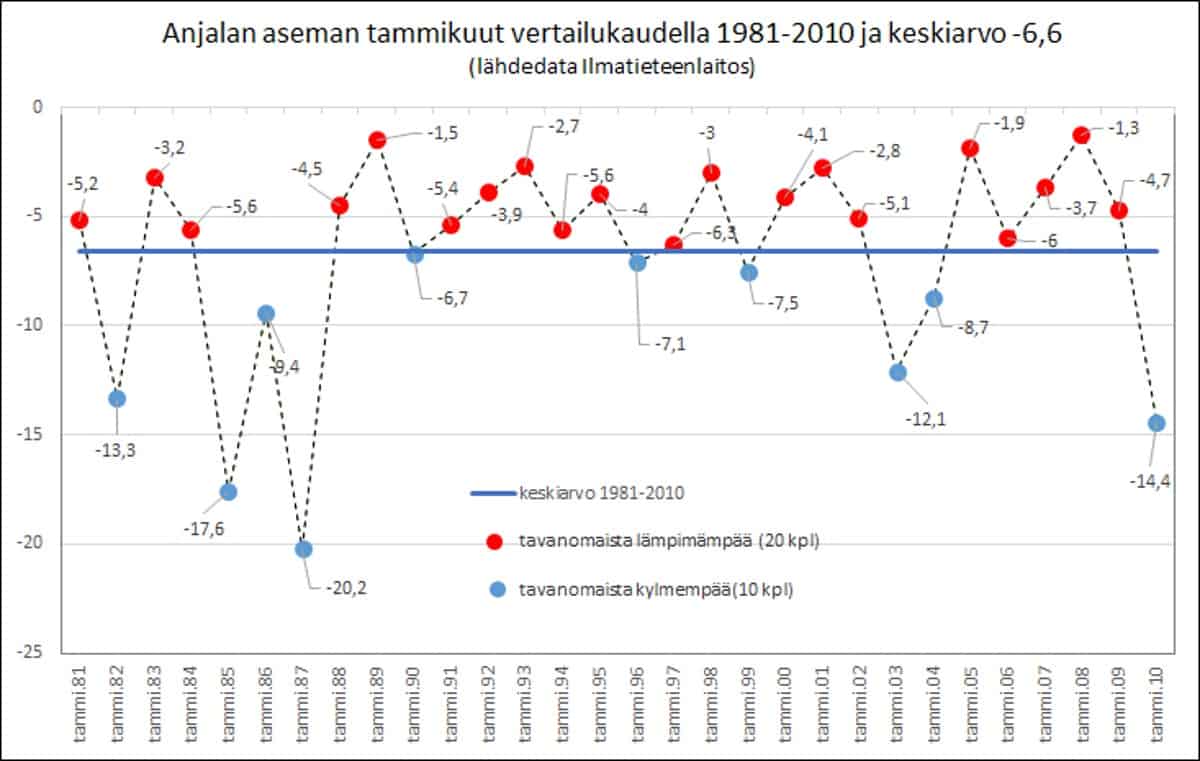
30 vuotinen keskiarvo näyttäisi osoittavan yleisimpien lämpötilojen viileintä rajaa, jättäen valtaosan yläpuolelleen keskiarvoa lämpimämmäksi.
Huomaamme, että keskiarvon yläpuolelle “tavanomaista lämpimämmäksi” asettuu kaksi kolmannesta havaintodatasta ja vastaavasti vain kolmannes kylmemmälle puolelle. On siis odotettavissa, että myöhempienkin aikojen lämpötiloja vertailtaessa saadaan keskiarvoa eli “tavanomaista” lämpimämpiä havaintoja useammin, vaikkei ilmasto olisi lainkaan lämmennyt. Keinulaudalla (kuva oikealla) näemme samantapaisen asetelman kuin aiemmassa Taanilan esimerkissä.
Geometrinen keskiarvo
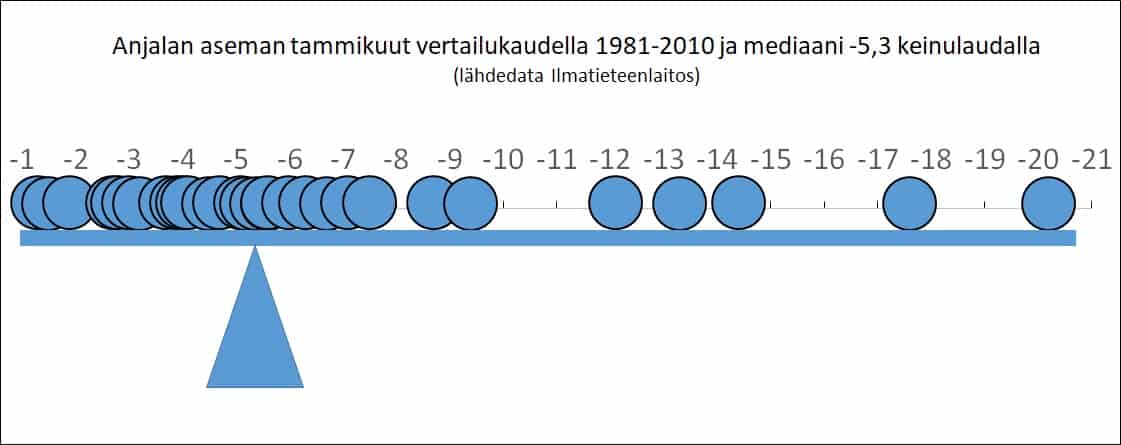Aritmeettisen keskiarvon sijaan päivämeteorologian vertailussa voitaisiin tietysti käyttää geometristä keskiarvoa eli mediaania. Siinä puolet havainnoista on korkeintaan mediaanin suuruisia ja puolet havainnoista on vähintään mediaanin suuruisia, keskiarvo on lukujen tulon n:s juuri (n on lukujen lukumäärä), kertoo ammattikouluaineisto netissä (http://www2.amk.fi/…/tutkimusme…/kvantitat/kuvailu/tunnu.htm).
Mediaanissa saisimme tasapuolisesti jakauman keskiarvon lämpimämmälle ja kylmemmälle puolelle, tiedä sitten, olisiko tämä fiksumpi tapa lämpötilojen vertailuun? “Tavanomaista lämpimämpää” saataisiin tietysti harvemmin, mutta vertailussa tulisimme lähemmäksi yleisimpiä lämpötiloja, joita kai myös sanamuodolla tavanomainen (tai keskimääräinen) haetaan?
Ilkka Ahmavaara 23.1.2019
